Pertama-tama sebelum kalian membaca, saya ingin memberi pesan untuk para pembaca terutama para "matematikawan". Di sini saya tidak akan terlalu rigor dalam membahas topik ini. Saya berusaha untuk membahas matematika di situs web ini sebagai bahan bacaan yang bisa dinikmati dengan menggunakan pendekatan seintuitif mungkin. Jadi, kalau kalian mau protes akan isi dari tulisan ini, silakan sampaikan di komentar biar rame, hehe.
Bacaan ini mengasumsikan pembaca adalah orang-orang yang sudah tamat SMA tapi yang masih sekolah juga bisa baca.
Bilangan adalah sesuatu yang digunakan manusia untuk mengukur. Satu, dua, tiga, empat, lima, dan seterusnya, kita gunakan bilangan asli untuk menghitung banyaknya benda. Konon, sejak zaman goa dulu, kita telah menghitung dengan bilangan asli. Ada pula yang namanya bilangan rasional seperti 1/2, 1/4, 2/3 dan lain-lainnya. Bilangan-bilangan ini biasanya dipakai untuk menunjukkan pecahan atau perbandingan.
Garis bilangan riil adalah suatu garis khayal, garis yang abstrak tempat semua bilangan-bilangan itu ada. Dari bilangan bulat, pecahan hingga irasional. Sudah menjadi kesepakatan, semakin ke kanan maka bilangan tersebut semakin besar. Setiap bilangan riil dapat dinyatakan dalam bentuk desimal yakni hanya dengan menggunakan simbol 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 serta tanda koma atau titik tergantung di mana kalian tinggal.
Semua bilangan riil terletak dalam suatu garis tanpa ujung. Bilangan-bilangan yang ada di sebelah kanan nol (0) adalah bilangan positif. Sedangkan, bilangan-bilangan yang ada di sebelah kiri 0 adalah bilangan negatif.
Mr. X
Muḥammad bin Mūsā al-Khawārizmī adalah orang yang mulai mempersembahkan metode super untuk menyelesaikan matematika. Suatu metode untuk mencari pecahan puzzle untuk menyelesaikan puzzle agar puzzle menjadi seimbang. Metode yang telah dikembangkan oleh umat manusia ini adalah salah satu batu loncatan yang sangat besar dalam perkembangan matematika, aljabar.
Dengan aljabar, kita bisa membahas sesuatu yang tidak kita ketahui dalam matematika. Hanya dengan memisalkan sang sesuatu dengan simbol x, kita bisa dengan sangat mudah untuk melakukan berbagai macam akrobat dalam matematika untuk mencari nilai dari si x atau mencari sifat-sifat lain dari si x.
Banyak jenis persamaan bisa kita selesaikan dengan aljabar, mulai dari persamaan linier, persamaan kuadrat, hingga persamaan kubik dan kuartik. Matematikawan sudah menemukan formula umum mencari solusi-solusi dari persamaan tersebut. Apakah benar begitu? Coba kalian bertanya-tanya, apakah persamaan berikut punya solusi?
x2 + 1 = 0
Dengan konsep timbangan, dengan mengurangi kedua ruas dengan 1, diperoleh
x2 = -1.
Apakah mungkin persamaan ini punya solusi? Andaikan ada bilangan riil x yang memenuhi persamaan tersebut tentu saja akan terjadi kontradiksi sebab bilangan kuadrat tidak pernah negatif. Ya, seperti itulah yang diberitahu guru saat SD, negatif dikali negatif hasilnya positif. Mungkin banyak dari tulisan ini dari atas sampai bawah berisi doktrin-doktrin yang disuap oleh guru ke kita. Terlepas dari keraguan dalam hati pembaca, alangkah baiknya tulisan di situs web ini cukup dinikmati saja tanpa perlu untuk dipercaya kandungannya.
Walaupun saya selaku penulis tidak menyarankan untuk percaya dari isi tulisan ini, di atas saya telah menulis bahwa para matematikawan sudah menemukan formula umum uintuk mencari solusi dari persamaan linier, kuadrat, hingga persamaan polinomial berderajat 4. Kalimat ini bukannya sudah terpatahkan oleh keberadaan persamaan x2 = -1? Jawabannya adalah tidak, sebab membuktikan suatu persamaan tidak punya solusi juga merupakan penyelesaian dari masalah mencari solusi. Kalau kalian mencari tikus di rumah agar kalian tidak diganggu tikus, tapi ternyata tikusnya memang benar-benar tidak ada, apakah kalian perlu mencari si tikus? Tentu saja tidak perlu, kalian hanya perlu tahu kalau tikusnya tidak ada dan masalah pun selesai.
Apakah Memang Benar Tidak Punya Solusi?
Ini bisa jadi plot twist dan bisa jadi bukan. Ini bukan plot twist bagi kalian yang sudah mengenal bilangan imajiner atau pernah dengar-dengar sedikit tentang bilangan imajiner. Plot twist-nya adalah ternyata x2 + 1 = 0 mempunyai solusi. Tidak, maksud saya bukan "terbukti tidak punya solusi" tapi maksud saya persamaan ini benar-benar punya solusi x. Kita sudah buktikan bahwa kalau x riil, maka x bukan solusi persamaan tersebut. Dengan demikian, solusinya pasti bukan berupa bilangan riil. Banyak orang bilang solusinya adalah suatu bilangan khayal, bilangan imajinasi yang diberi nama dan simbol i. Jadi,
i2 + 1 = 0 atau i2 = -1. Ini adalah plot twist bagi kalian yang tidak pernah mendengar tentang bilangan ini. Mungkin terdengar curang, tiba-tiba kita bisa buat bilangan baru untuk dijadikan solusi dari suatu persamaan yang harusnya kan tidak punya solusi. Kemudian, kita beri sebut bilangan tersebut adalah bilangan khayal tanpa rasa bersalah. Bagi kalian yang skeptis akan keberadaan bilangan imajiner, kalian juga saya rekomendasikan silakan skeptis walaupun sebentar akan keberadaan bilangan riil. Apakah bilangan benar-benar? Ehem, itu menjadi PR (pekerjaan rumah) untuk sementara, saya sudah bilang silakan enjoy dulu dan tahan rasa skeptis itu atau mungkin kalian bisa cari di Google (kalau masih ada), siapa tahu bisa menemukan pencerahan.
Dimanakah i?
Lalu, apa gunanya bilangan imajiner? Itu kan hanya bilangan khayal. Fufufu, jangan naif kawan-kawan. Justru dengan kekuataun imajinasi 🌈, banyak masalah baik dalam bidang matematika bahkan hingga sains bisa diselesaikan lebih mudah dengan adanya bilangan imajiner ini karena sesungguhnya bilangan imajiner ini mungkin sebenarnya lebih nyata daripada yang kita bayangkan. Namun, untuk sekarang mungkin tidak akan saya kasih tahu apa saja manfaatnya biar kalian semakin penasaran dan mulai mencari-cari referensi, hehehe.
Kita akan segera menuju plot twist yang selanjutnya. Apa? Ada plot twist lagi? Ingat bahwa bilangan riil punya posisinya masing-masing di garis bilangan. Nah, kira-kira si bilangan imajinasi i ini ada di mana yah?
Dimana yah? Apakah ada di sebalah kanan 3 gitu? Atau mungkin ada di sekitar -1 gitu, kan kalau dikuadratkan hasilnya adalah -1?
Jawabannya adalah ....
i tidak ada di garis bilangan riil karena i bukan bilangan riil. Lebih jauh, i bukanlah bilangan positif yang arahnya ke kanan 0 atau bilangan negatif yang arahnya ke kiri 0. Hey, tunggu dulu. Kalau gak ada di kanan dan gak ada di kiri, terus dimana dong? i juga bukan 0 ya, kan? Dimana kira-kira i berada? Petunjuknya adalah judul dari tulisan ini. Yaps, bisa ke atas atau ke bawah, tapi kita sepakati saja i-nya ada di arah atas 0, mengingat kesimetrisan. Kalau kita mau cari tikus dan ternyata tikusnya tidak ada di dalam rumah, maka tentu saja kita harus mencarinya di luar rumah. i ada di luar garis bilangan riil.
Lihat apa yang terjadi, kita berhasil memperluas daerah tempat kita menaruh bilangan-bilangan yang awalnya hanya garis, sekarang kita sudah punya bidang. Kita sudah meletakkan semua bilangan riil di garis bilangan riil. Kita juga sudah meletakkan bilangan i di posisinya. Terus, di tempat-tempat kosong lain isinya apa yah? 🤔
Kira-kira apa yang terjadi kalau kita mengalikan i dengan bilangan riil. Contohnya saja 2 ✕ i, apakah
2 ✕ i adalah suatu bilangan? Ya, anggap saja itu bilangan juga dan kita tulis saja 2i. Semua perkalian dari i dengan bilangan riil kita sebut sebagai bilangan imajiner. Jadi, semua bilangan imajiner dapat dinyatakan dalam bentuk ai dengan a adalah bilangan riil. Selain itu, kita juga bisa menambah dan mengurang bilangan riil dan bilangan imajiner, misalnya saja 2 + 3i dan 5 - 4i. Hasil penjumlahan dan pengurangan bilangan riil dan bilangan imajiner ini kita sebut sebagai bilangan kompleks. Jadi bilangan kompleks adalah bilangan yang dapat dinyatakan dalam bentuk a + bi dengan a dan b adalah bilangan rii. Perhatikan bahwa a - bi sama saja dengan a + (-b)i. Oh yah, kalau b-nya adalah 0 maka
a + bi = a + 0i cukup ditulis a saja dan bilangan ini adalah bilangan kompleks sekaligus bilangan riil, yaps, bilangan riil adalah bilangan kompleks dengan komponen imajiner 0. Sedangkan jika a-nya 0, cukup ditulis bi saja, ini juga bilangan kompleks sekaligus bilangan imajiner.
Wow wow wow, dari masalah x2 + 1 = 0 kita bisa memperoleh konsep bilangan baru yang bernama bilangan kompleks. Sebenarnya sih berdasarkan sejarah, bukan karena masalah ini yang membuat konsep bilangan kompleks itu muncul. Ada masalah yang lebih rumit lagi yang benar-benar menjadi pemicu penemuan bilangan kompleks ini. Namun, di tulisan ini, kita tidak akan membahasnya.
Lalu, di manakah posisi bilangan-bilangan kompleks tersebut? Kalau 2i sepertinya wajar yah searah dengan i (yakni ke atas) dengan jaraknya bersama 0 menjadi 2 kali lipat.
Semua bilangan imajiner terletak pada garis vertikal yang dinamakan garis bilangan imajiner. Jadi, garis horizontal adalah garis bilangan riil sedangkan garis vertikal adalah garis bilangan imajiner.
Kemudian, bagaimana dengan bilangan kompleks yang lain? Hmm, tebakan bagus, tentu saja tiap dari mereka ada di salah satu keempat kuadran. Misalnya saja 3 + 2i ada disini.
Bayangkan kita berjalan dari 0 ke titik 3 + 2i. Untuk sampai ke titik 3 + 2i, kita cukup ke arah kanan sejauh 3 satuan, kemudian ke atas sejauh 2 satuan. Hmm, apakah ini kelihatan sedikit familiar? Ini mirip dengan koordinat kartesius, bukan? Bahkan kalau kita perhatikan penjumlahan bilangan kompleks, ia sangat mirip dengan penjumlahan vektor. Wah, wah, wah, kebetulan macam apakah ini? Apakah bilangan kompleks juga berguna dalam menyelesaikan masalah vektor? Jawabannya adalah .... iya 😄 Masalah vektor dan geometri bisa diselesaikan dengan mudah dengan bilangan kompleks. Sebaliknya juga, masalah bilangan kompleks dapat pula diselesaikan dengan geometri. Sangat mencengangkan, bukan? Ternyata bilangan imajiner lebih nyata daripada namanya.
Kita bisa menganggap bilangan kompleks sebagai bilangan 2 dimensi karena berada dalam suatu bidang sebagaimana bilangan riil adalah bilangan 1 dimensi karena berada dalam suatu garis.
Bentuk Polar Bilangan Kompleks
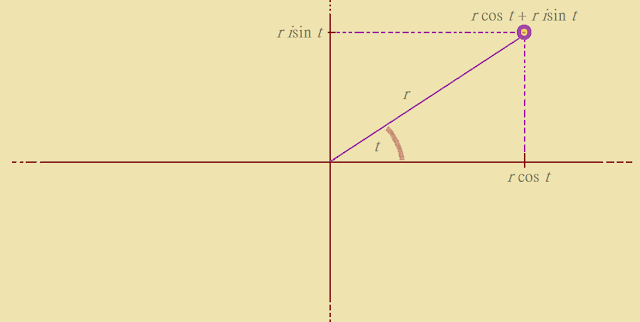
Kita sudah tahu bahwa bilangan kompleks terletak pada suatu bidang yang akan kita sebut sebagai bidang kompleks. Jadi, bilangan kompleks a + bi posisinya sama seperti posisi titik (a,b) di bidang kartesius. Mirip seperti vektor (matematikawan umumnya juga menganggap bilangan kompleks adalah vektor), bilangan kompleks mempunyai arah dan panjang. Setiap bilangan kompleks dapat dinyatakan dalam bentuk polar sama seperti vektor yang bisa dinyatakan dalam panjang dan sudut yang dibentuknya.
Jadi, setiap bilangan kompleks z = a + bi dapat dinyatakan sebagai z = rcos t + risin t atau
z = r(cos t + isin t), dengan r adalah jarak bilangan kompleks z dengan 0 dan t adalah besar sudut yang terbentuk antara garis z0 sebagai sisi terminal dan sumbu x sebagai sisi inisial (sisi awal). Jadi,
a = r cos t dan b = r sin t. r disebut sebagai modulus dari bilangan kompleks z dan dinotasikan
|z| = r.
Dengan menggunakan teorema legendaris yakni Teorema Pythagoras, misalkan bilangan kompleks
z = a + bi dengan a, b adalah bilangan riil, maka modulus dari z adalah
|z| = (a2 + b2)1/2.
Mohon maaf untuk sekarang saya belum pakai LaTeX dulu yah. 😉
Dalam bentuk polar, bilangan kompleks lebih mudah dikalikan. Saat dua bilangan kompleks dikali, modulusnya dikalikan dan sudutnya ditambah. Jadi, misalkan dua buah bilangan kompleks
z1 = r1(cos t1 + isin t1), dan
z2 = r2(cos t2 + isin t2),
maka hasil perkaliannya adalah
z1z2 = (r1r2)(cos (t1 + t2) + isin (t1 + t2)).
Untuk buktinya bisa kalian cari di Google, hehe atau kalian bisa lihat di tulisan saya selanjutnya.
Formula De Moivre
Dengan menggunakan sifat perkalian bentuk polar bilangan kompleks, kita bisa dengan mudah mengalikan bilangan kompleks yang sama berkali-kalian atau dengan kata lain sangat mudah memangkatkan bilangan kompleks dengan bilangan asli. Misalkan z = r(cos t + isin t) maka diperoleh
z2 = r2(cos 2t + isin 2t).
Secara umum, untuk setiap bilangan asli n berlaku
zn = rn(cos nt + isin nt).
Ini juga dapat dibuktikan berlaku untuk n bulat negatif.
Untuk sekarang, kita simpan dulu formula De Moivre di sini yah. 😁
Solusi Bilangan Kompleks Persamaan
Okay, coba kita perhatikan persamaan berikut.
x4 = 1
Kira-kira ada berapa yah solusi dari persamaan tersebut? Bilangan apa yang apabila dipangkatkan 4 hasilnya adalah 1? Kalau kalian jawab ada sebanyak 2, kalian benar. Tentu, kalau yang kalian maksud itu solusi bilangan riil. Bilangan riil yang menjadi solusi persamaan tersebut hanyalah 1 dan -1. Namun, tahukah kalian bahwa persamaan tersebut mempunyai 4 solusi bilangan kompleks? Tidak percaya? Selain 1 dan -1, solusi lainnya adalah i dan -i.
Ternyata persamaan tersebut tidak hanya punya 2 solusi saja tapi punya 4 solusi bilangan kompleks. Fakta menarik lainnya adalah persamaan xn = 1 dengan n adalah bilangan asli mempunyai tepat n solusi bilangan kompleks, wow.
Saat kita berbicara bilangan kompleks sebagai solusi dari persamaan, kita bisa memperoleh lebih banyak solusi daripada hanya berbicara tentang bilangan riil.
xn = 1
Persamaan ini adalah persamaan yang cukup menarik sehingga dijadikan segmen tersendiri dalam tulisan ini. Keunikan dari persamaan ini adalah apabila n ≥ 3, saat kita mem-plot semua solusi di bidang kompleks. Gambarnya adalah titik-titik yang terletak pada lingkaran dan posisinya simetris sedemikian sehingga menjadi titik-titik sudut pada segi-n beraturan.
Solusi dari x4 = 1 adalah, 1, -1, i, dan -i. Berikut adalah gambarnya.
Kalian bisa coba cari solusi dari xn = 1 untuk n yang lain. Bagaimana cara melakukannya? Clue-nya adalah kalian bisa gunakan De Moivre dan ingat fungsi trigonometri sinus dan kosinus bersifat periodik.
Solusi dari xn = 1
Di bagian ini saya akan menjelaskan lebih detail gimana cara mencari solusi dari xn = 1. Pertama-tama kita pakai contoh kecil saja misal x4 = 1. Perhatikan bahwa
1 = 14(cos 0 + isin 0) = 14(cos (4•0) + isin (4•0)).
Ini sangat familiar bukan? Ini mirip dengan formula De Moivre di atas dengan n = 4. Misalkan x adalah bilangan kompleks dengan bentuk polar r(cos t + isin t). Agar x bisa menjadi solusi dari x4 = 1 maka panjang dari x yakni r haruslah sama dengan 1. Jadi x = cos t + isin t. Okay, kembali ke De Moivre tadi. Agar x menjadi solusi dari x4 = 1 maka haruslah
x4 = 14(cos (4•t) + isin (4•t)) = 1 = 14(cos (4•0) + isin (4•0)).
Dari sini dapat diamati dengan jelas bahwa kita memperoleh salah satu solusi x dengan t = 0 yakni solusi trival x = 1. Lalu, darimana solusi yang lain?
Ingat bahwa fungsi trigonometri kosinus dan sinus itu berperiodik (berulang setiap 2ℼ). Kita juga dapat menulis 1 sebagai
1 = 14(cos 2ℼ + isin 2ℼ) = 14(cos (4•½ℼ) + isin (4•½ℼ))
Dari sini lagi kita bisa lihat bahwa solusi lain dari x4 = 1 adalah
x = cos (½ℼ) + isin (½ℼ) = 0 + i(1) = i.
Nah, untuk 2 solusi terakhir, perhatikan bahwa
1 = 14(cos 4ℼ + isin 4ℼ) = 14(cos (4•ℼ) + isin (4•ℼ))
dan
1 = 14(cos 6ℼ + isin 6ℼ) = 14(cos (4•(3/2)ℼ) + isin (4•(3/2)ℼ)).
Jadi, t juga bisa ℼ dan bisa juga (3/2)ℼ. Ini memberikan solusi secara berturut x = -1 dan x = -i.
Bagaimana kalau sudutnya ditambah 2ℼ lagi? Apakah akan muncul solusi baru? Jawabannya adalah tidak.
1 = 14(cos 8ℼ + isin 8ℼ) = 14(cos (4•2ℼ) + isin (4•2ℼ))
Malahan, kita bakalan balik ke solusi pertama, yakni solusi x = 1. Kalau kita tambahkan 2ℼ terus menerus, yang terjadi hanya muter saja dari keempat solusi yang sudah kita temukan tadi.
Saya harap kalian bisa paham dari tulisan saya ini. Dari sini kita bisa melihat pola bahwa solusi
xn = 1 adalah
x = cos (2ℼk/n) + isin (2ℼk/n) dengan k adalah bilangan bulat. Nah, nanti akan nemu sebanyak n solusi berbeda. Jadi, cukup ambil saja k-nya dari 0, 1, 2, dan seterusnya sampai n - 1 karena kalau k-nya yang diambil lebih dari n - 1 nanti balik lagi ke solusi pertama lalu akan muter lagi. Begitupun kalau kita ngambil k bulat negatif. Tentu saja, ini harus dibuktikan dan jadi PR bagi pembaca sekalian. Kalian bisa gunakan De Moivre untuk membuktikannya.
Latihan Soal
Mari kita latihan soal ya teman-teman. Misalkan kita punya dua buah himpunan.
A = {z ∈ ℂ : z6 = 1}
B = {z ∈ ℂ : z9 = 1}
Saya harap para pembaca sudah paham notasi himpunan. Intinya sih himpunan A adalah himpunan solusi bilangan kompleks dari persamaan z6 = 1 dan himpunan B adalah himpunan solusi bilangan kompleks dari persamaan z9 = 1. Bagi kalian yang sampai di sini kurang paham, kalian bisa skip saja tulisan ini lalu baca tulisan saya selanjutnya.
Nah, sebagian orang pasti sudah selesai mengerjakan soal ini. Mungkin kalian heran? Lah, kok bisa padahal soalnya belum ada? Tentu saja soalnya belum saya kasih tapi anehnya banyak orang yang hanya dikasih beberapa persamaan tiba-tiba dengan ajaibnya bisa "menyelesaikan" "soal"nya padahal soalnya tidak ada. Fenomena aneh ini bakalan saya bahas di tulisan berikut-berikutnya. Intinya mereka adalah orang-orang yang tidak paham, yang mereka lihat hanyalah simbol-simbol yang bisa "diselesaikan", mereka bagaikan kalkulator yang berwujud manusia, berusaha menyelesaikan suatu masalah yang mereka anggap ada tapi tidak tahu masalahnya apa. Jika kalian tidak paham dengan simbol-simbol matematika, sebaiknya kalian skip saja. Jangan berusaha "menyelesaikan" soal yang tidak kalian paham bahkan belum tentu ada.
Soalnya simpel banget sih.
Berapa banyak anggota dari A∪B, yakni gabungan dari A dan B?
Soal ini bisa kalian selesaikan dengan mudah kalau kalian paham dengan De Moivre.
Jawaban dari soal ini akan saya tulis di tulisan berikutnya. Oh yah, saya peringatkan bahwa banyak anggota gabungan dua buah himpunan tidak serta merta diperoleh dengan menjumlahkan banyak anggotanya.
















Tidak ada komentar:
Posting Komentar